The Pokémon Graph Cover Problem
Prerequisites
Before starting, readers should
- have a working knowledge of C++ and the most common STL data structures such as
std::vector. - be familiar with graph theory as it relates to computer science, specifically exact cover problems.
- briefly explore Donald Knuth’s work on Dancing Links (DLX) solvers.
- be familiar with the binary representation of numbers.
- be familiar with lexicographic order.
Outline
By the end of this post, readers will
- understand the basics of Dancing Links and exact cover problems.
- be able to model Pokémon type interactions as an exact cover problem.
- see the benefits of C++ class design for modeling the Pokémon exact cover problem.
Note: This article is based on a project I implemented in C++. The full code related to the segments shown can be found in my GitHub repository.
Exact Cover
Here is the formal definition of an exact cover as given by Wikipedia.
Given a collection
Sof subsets of a setX, an exact cover ofXis a sub-collectionS*ofSthat satisfies two conditions:
- The intersection of any two distinct subsets in
S*is empty, i.e., the subsets inS*are pairwise disjoint. In other words, each element inXis contained in at most one subset inS*- The union of the subsets in
S*isX, i.e., the subsets inS*coverX. In other words, each element inXis contained in at least one subset inS*.
Donald Knuth has a neat solver for this problem that he calls Dancing Links (in 2024 Knuth gave a talk where he suggests a new method called Dancing Cells may be preferred for exact cover problems, but I do not cover that in this post). The namesake for the algorithm comes from how it models the connections a graph forms (the edges) and options we have to choose from that form those connections (the nodes).
The algorithm uses a grid of doubly linked lists to model the graph relationships. The rows represent the set of connections for a given vertex in the graph, and the columns illustrate overlap between sets of connections for each of the vertices.
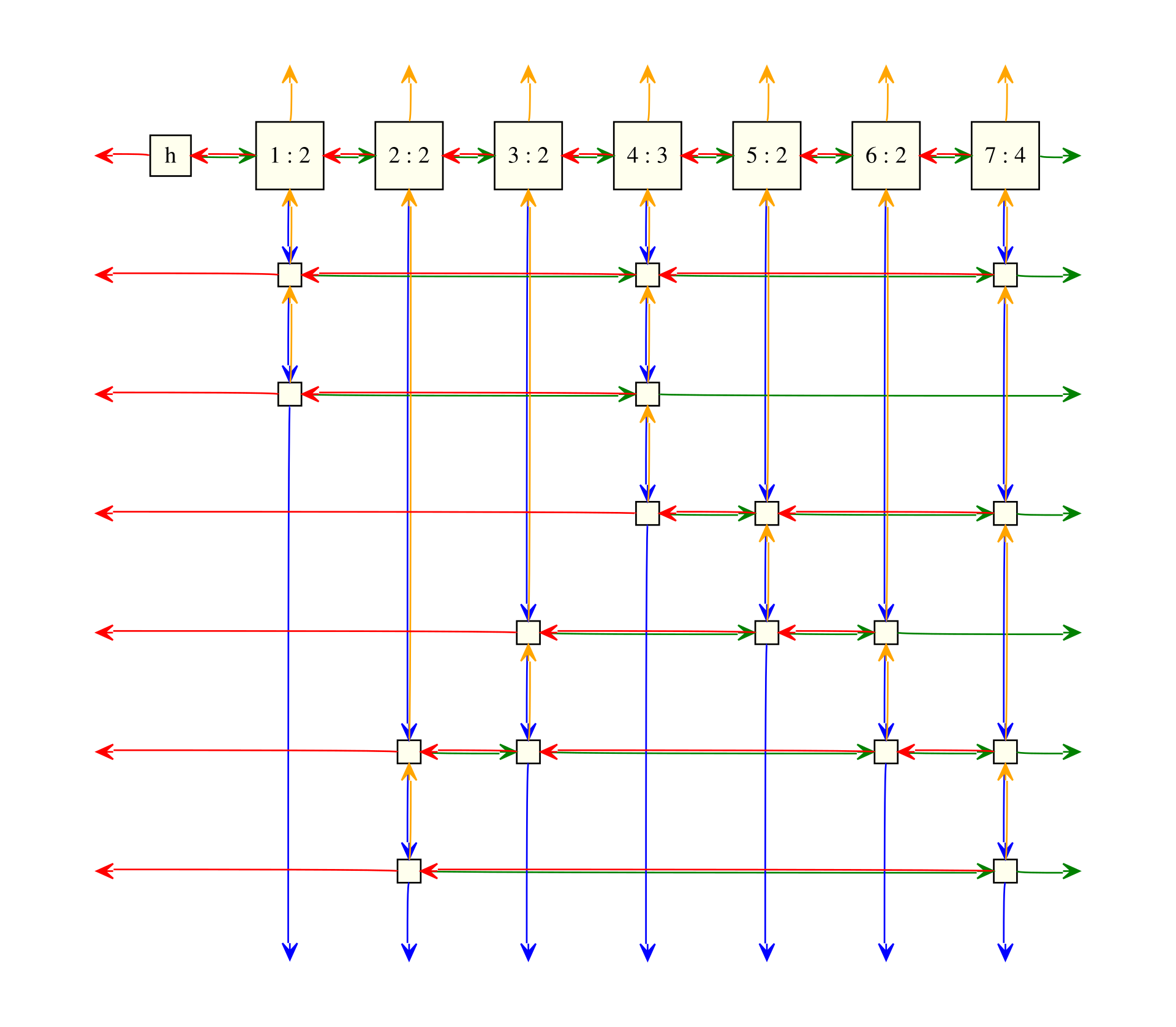
Image provided by Fschwarzentruber under the Creative Commons Attributionn-Share Alike 4.0 license.
The goal of the algorithm is then to choose a node in a row that will cover other nodes in the matrix. When a node is selected, all items in a row are spliced out of their respective doubly linked lists. In addition, we eliminate the entire column for each node in the row we have selected and all rows in each of those columns; this ensures the exactness of the cover solution.
The key insight of Dancing Links is that when these splices occur the spliced out nodes retain their pointers such that we can recursively restore links during the backtracking phase: thus the links dance during the branching search for a solution. The problem is solved if the grid becomes empty, meaning there are no rows or columns remaining. I understand if this is confusing for now. The examples that follow will walk through every step of reducing the grid size.
In October 2022, Donald Knuth released The Art of Computer Programming: Volume 4b: Combinatorial Algorithms, Part 2. In this work, he revised his previous implementation of his Algorithm X via Dancing Links. His revision included changing the quadruple linked nodes that solved backtracking problems to an array of nodes. This is an interesting optimization. It provides good locality, ease of debugging, and memory safety if you use an array that does not need to be managed like a C++ vector. One of the points Knuth makes clear through his section on Dancing Links is that he wants to give people the tools they need to expand and try his backtracking strategies on many domains. If you want the full, original Algorithm, please read Knuth’s work. Below, I will discuss how I applied or modified his strategies to fit a fun puzzle I have often considered for the game of Pokémon.
Types and Teams
Knuth brings up many puzzles in his work on combinatorial algorithms. He has word puzzles, number puzzles, literal puzzle puzzles. All of these applications of DLX got me thinking about more problems I could find that use his methods, and I found one! The video game Pokémon by developer Game Freak is part of a well established franchise that started in the 1990s. At their core, the Pokémon video games are a game of rock-paper-scissors with a few dozen layers of complexity added on top. While I can’t explain the entire rule set of Pokémon here, I can explain the relevant parts to the abstraction I decided to solve.
In Pokémon, trainable creatures battle on your behalf imbued with pseudo-elemental types like fire, water, flying, ground, and many others. There are 15 to 18 fundamental types that Pokémon can use, depending on the generation of games you are considering. Because Pokémon has been around for so many years, they have made many changes to their games. The community that plays those games often divides the games by generations in which different game mechanics were introduced. I worked on this project when there were nine generations. At the most abstract level, you only need to consider how to attack other Pokémon with these fundamental types and how to defend against these attack types with your own Pokémon. The twist on defense is that your Pokémon can have up to two different types–such as Fire-Flying or Ice-Water–that determine how weak or resistant they are to these fundamental attack types.
These fundamental types could be combined to form 306 dual types if we count dual types in different orders as different types, not to mention the additional 15 to 18 single types. However, the developers of this game have not done this yet. Depending on the generation, there are far fewer types than this, but there are still many. Generation nine is up to 162 unique Pokémon types.
So, there are two cover problems hiding in the complexities of the Pokémon games: one for defense and one for attack. The two essential cover questions we can ask are as follows.
- Which teams of at most 6 Pokémon–the most you can carry with you at once–give me resistance to every attack type I will encounter? If you consider an entire game, you would want to know the answer to that question for every attack type in the game. If you are considering just the attacks you will face in some portions of the game, then the range of attack types shrinks, but the question remains the same.
- Which attack types can I choose to be effective against every defensive type I will encounter in the game? Each of the six Pokémon in a team can learn four attacks so that is 24 attack slots available. This is more than we need as there are at most 18 attack types to select from in any generation. Again, considering the entire game versus some smaller sections will change the range of defensive types you will see, but the question remains the same.
To try to answer these questions, we can begin to organize Pokémon’s data with Knuth’s dancing links method.
Defense
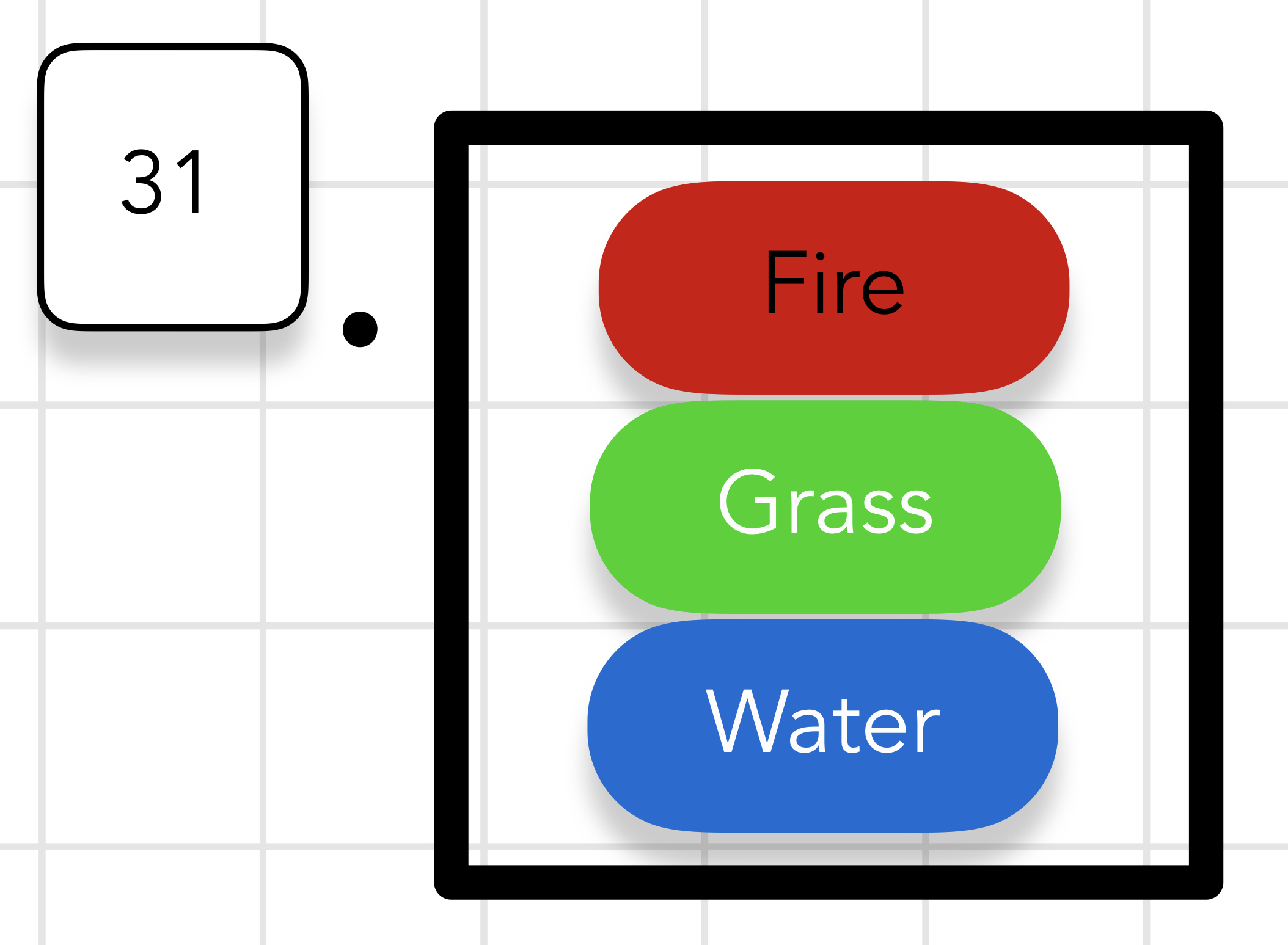
Let’s start with the defensive case. Here is a small subset of both attack and defensive types we can look at as a toy example.
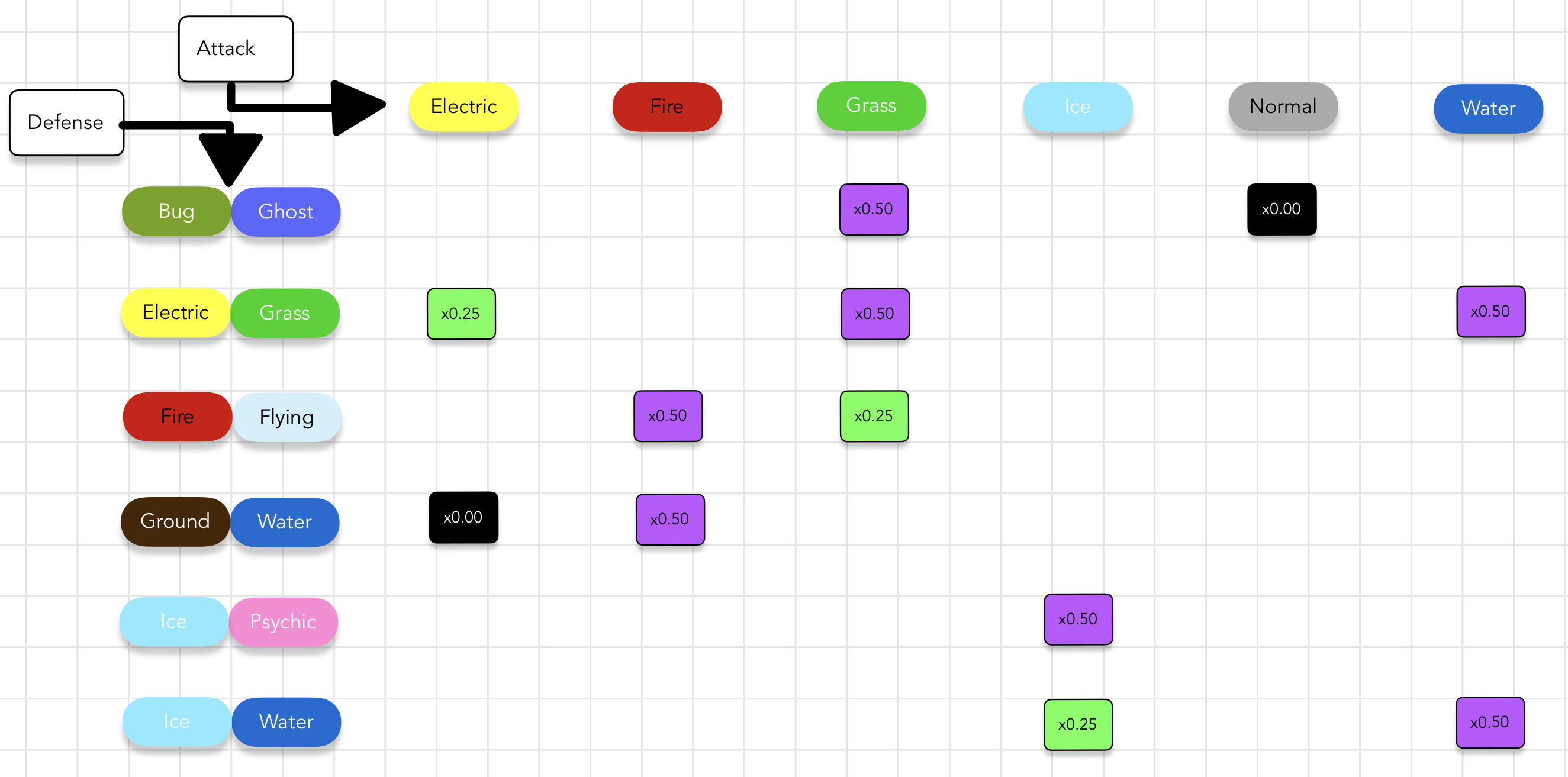
Here are the key details from the above image.
- Attack types we need to cover are our items, and defensive types we can use to resist those attack types are our options.
- There are different levels of resistance that types can have to attack types. You can think of resistances as fractional multipliers that are applied to what would otherwise be normal damage. The best we can do is nullify damage by being immune to that type. You can see this in the cases of Ground-Water vs Electric and Bug-Ghost vs Normal type attacks. A
x0.25multiplier is the next best followed by ax0.50. - While single defense types exist, I am not including them here to avoid confusion.
- The order of the two types in a dual type does not change any resistance or weakness to attack types. I organize all dual-types alphabetically for consistency.
To solve an exact cover version of the defensive problem, as Knuth describes in his work, we want to resist each of these attack types exactly once across the options we choose. You can take a moment to try to pick the types that achieve this before we go over the selection process.
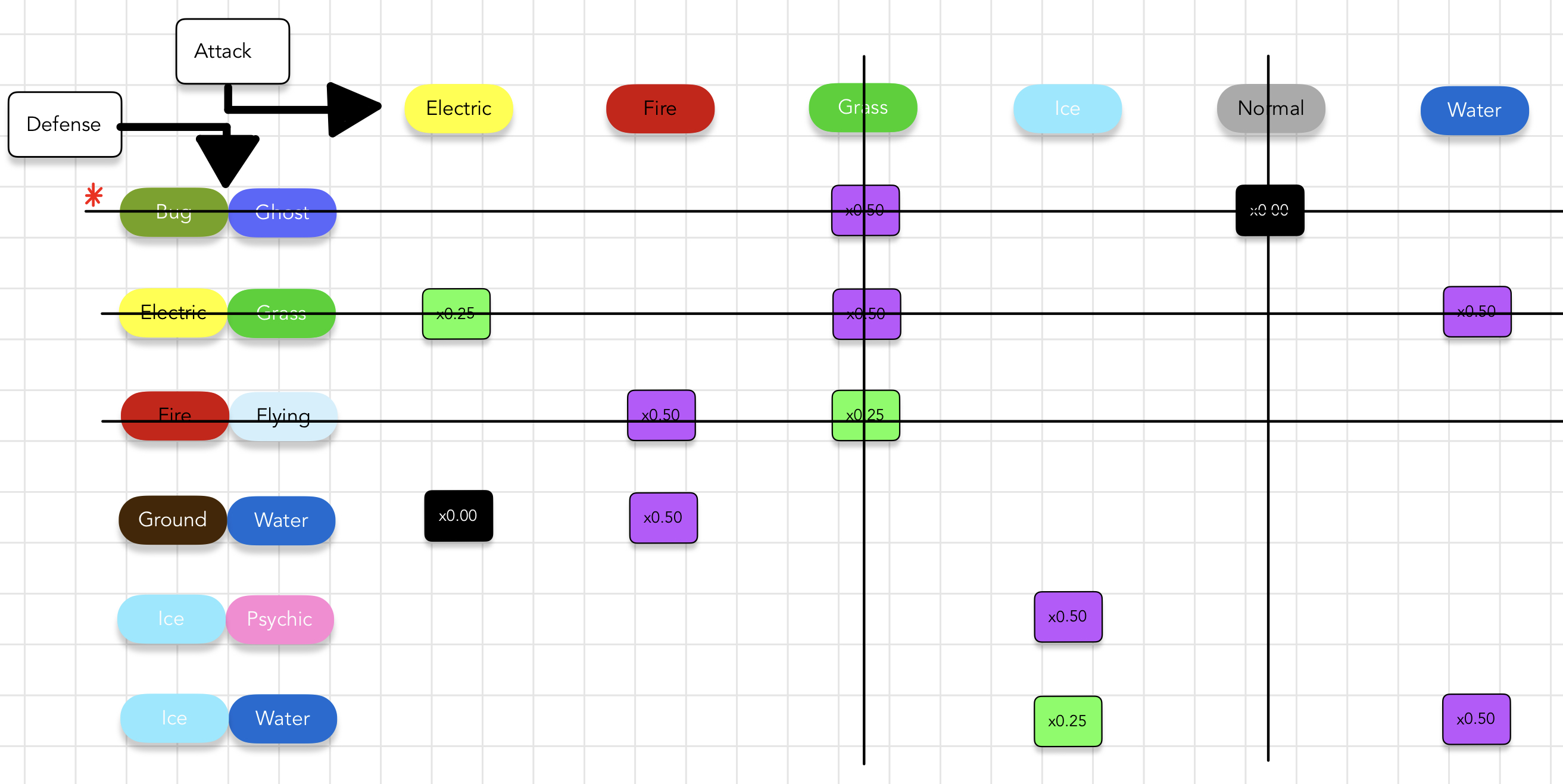
Here are the key details from the above image.
- We start by trying to cover an attack type that appears the least across all options, Normal. We pick option
Bug-Ghost. - This choice eliminates
Bug-Ghostand any other options that contain the attack itemsGrassandNormal; those items have already been covered by our current choice.
We are then left with a shrunken grid to consider solving.
If we follow the same selection and elimination process, we are led to the following solution.
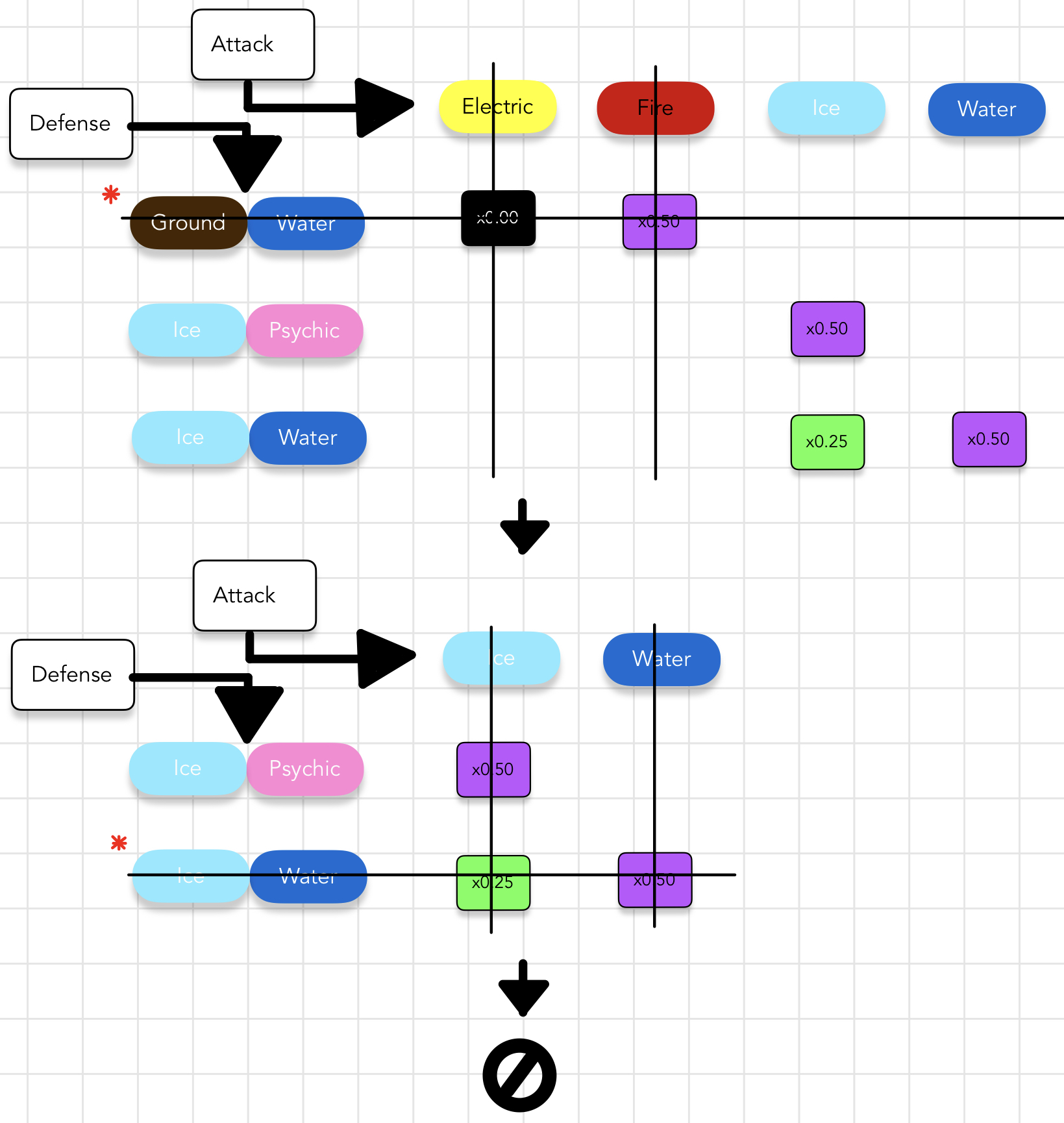
Here are the key details from the above image.
- Our remaining two selections are marked with the red asterisk.
- We know we have solved the problem when no items remain in the world.
- The heuristic of selecting an item that appears few times across all options will often decrease the number of iterations of this algorithm.
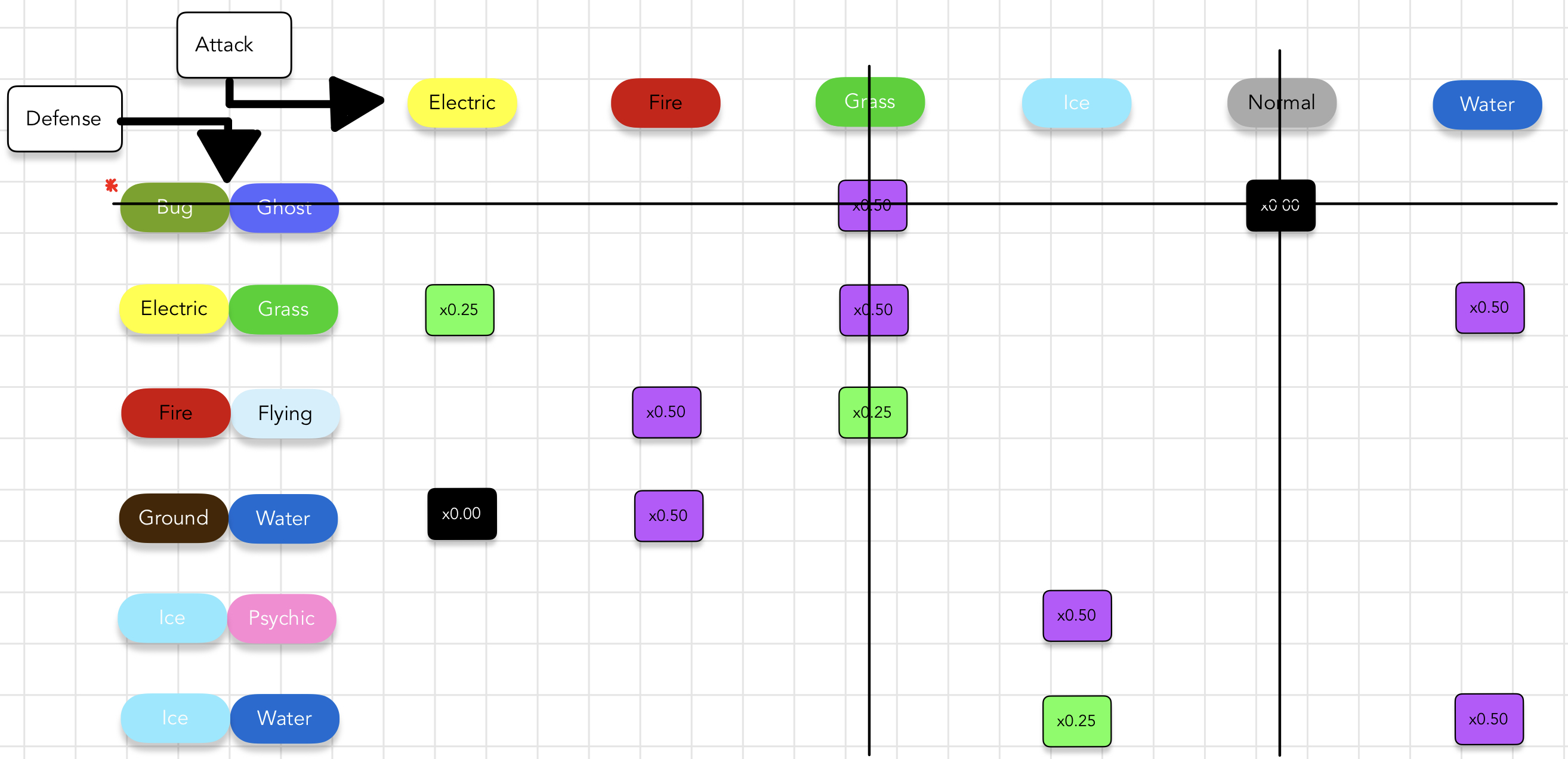
While it is good to see how quickly this process shrinks the problem, it can sometimes be hard to see what about this selection process makes it an exact cover. To help visualize the exact nature of these choices, here is another way to look at the cover solution.
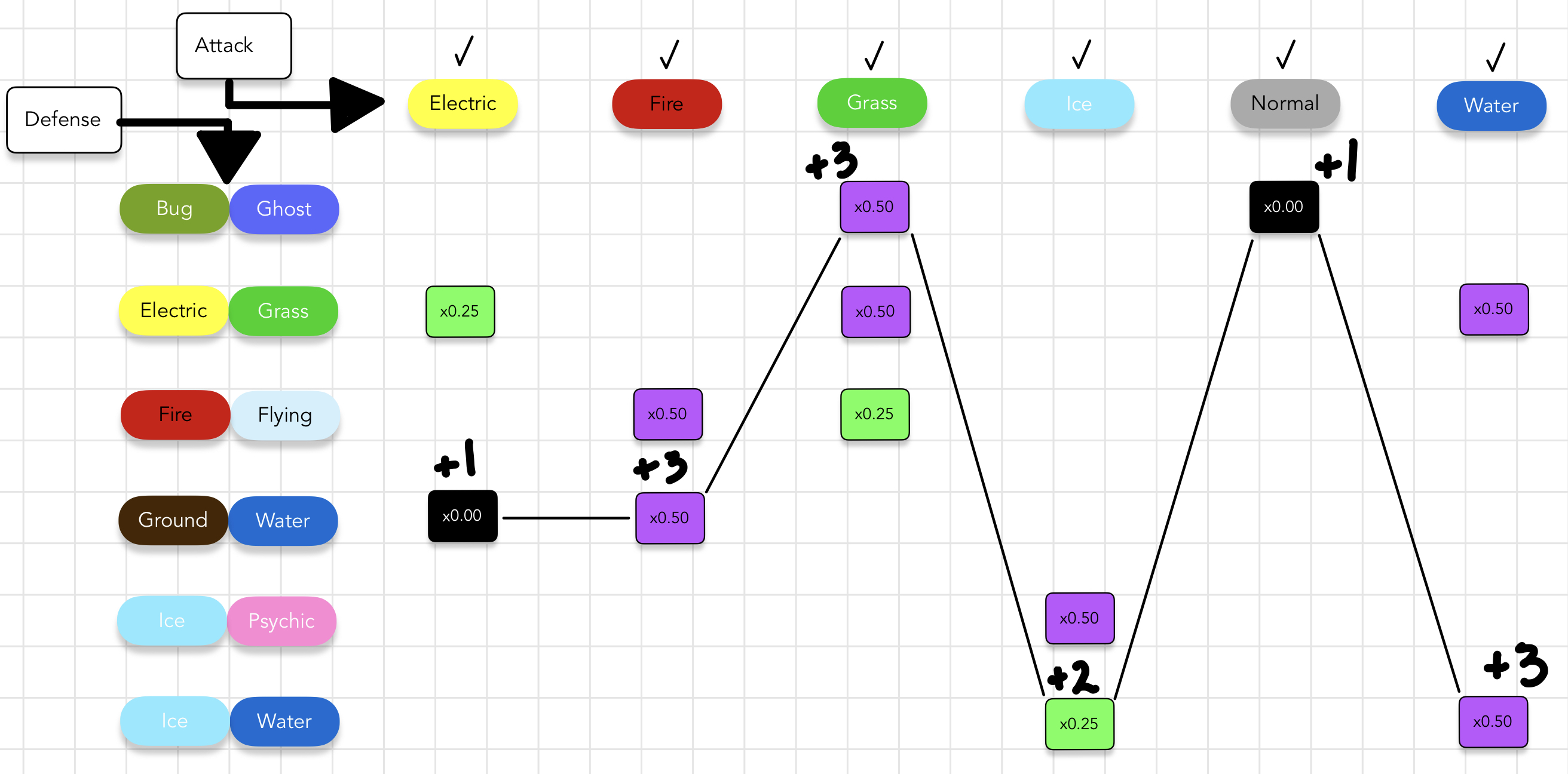
Here are the key details from the above image.
- No two defensive types that we chose covered the same attack type. I find it easier to think of this as a perfect walk across the items from left to right with no wasted steps, as illustrated by the line I take through these items.
- In addition to finding all solutions, I rank the covers that I find according to a scoring system for defense.
- The
x0.00multiplier is1 point. - The
x0.25multiplier is2 points. - The
x0.50multiplier is3 points. - A LOWER score is better than a higher score. This favors stronger resistances.
- The
- This scoring systems is an arbitrary product of my implementation based on what I assume is good in these games. I haven’t thought critically about Pokémon in quite some time, so maybe an expert could provide more guidance here.
All choices considered, here is the final score of our exact cover team of 3.
In such a small case the significance of this score may not be apparent, but when generating thousands of solutions it can become helpful to sift through them with a ranking system. Let’s now look at Attack.
Attack
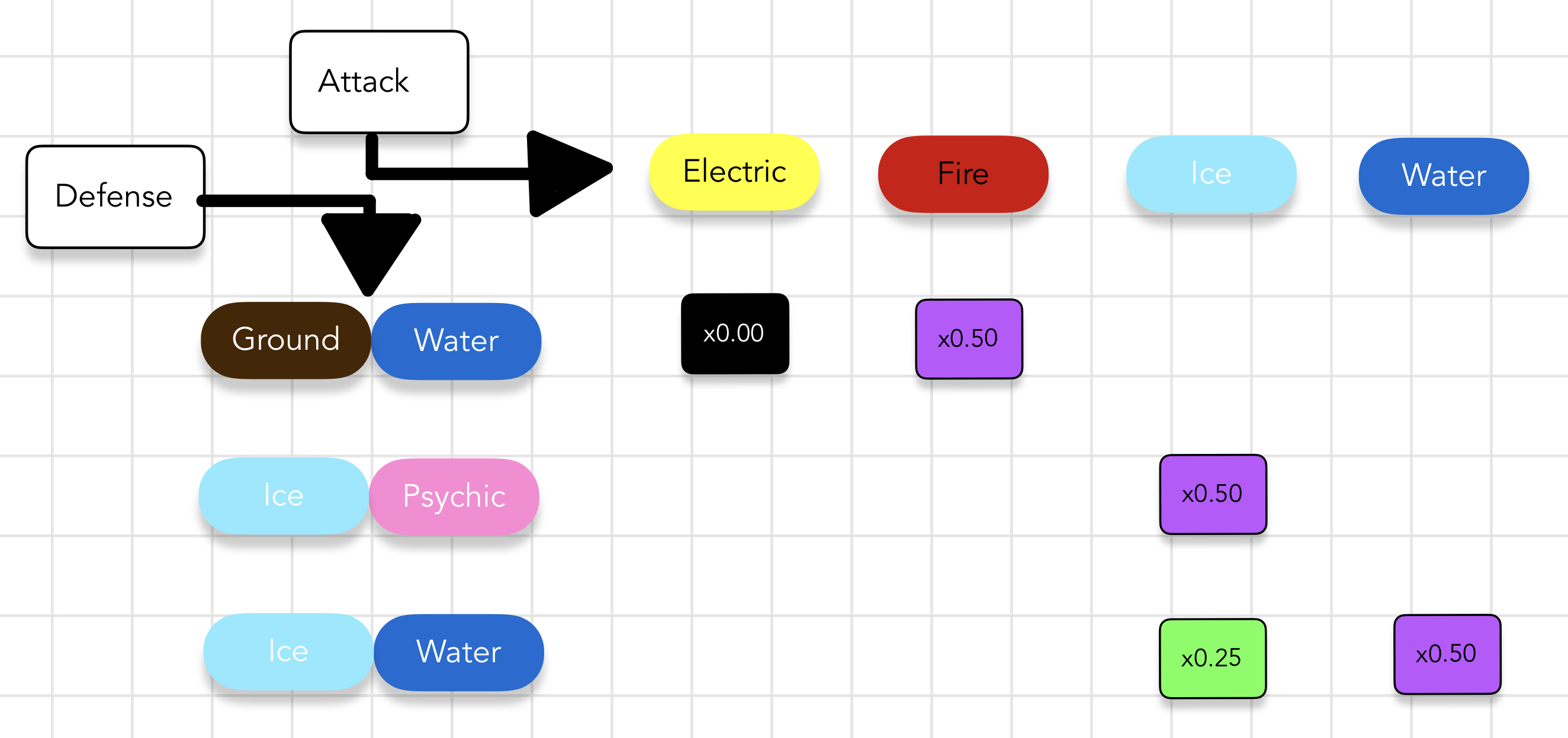
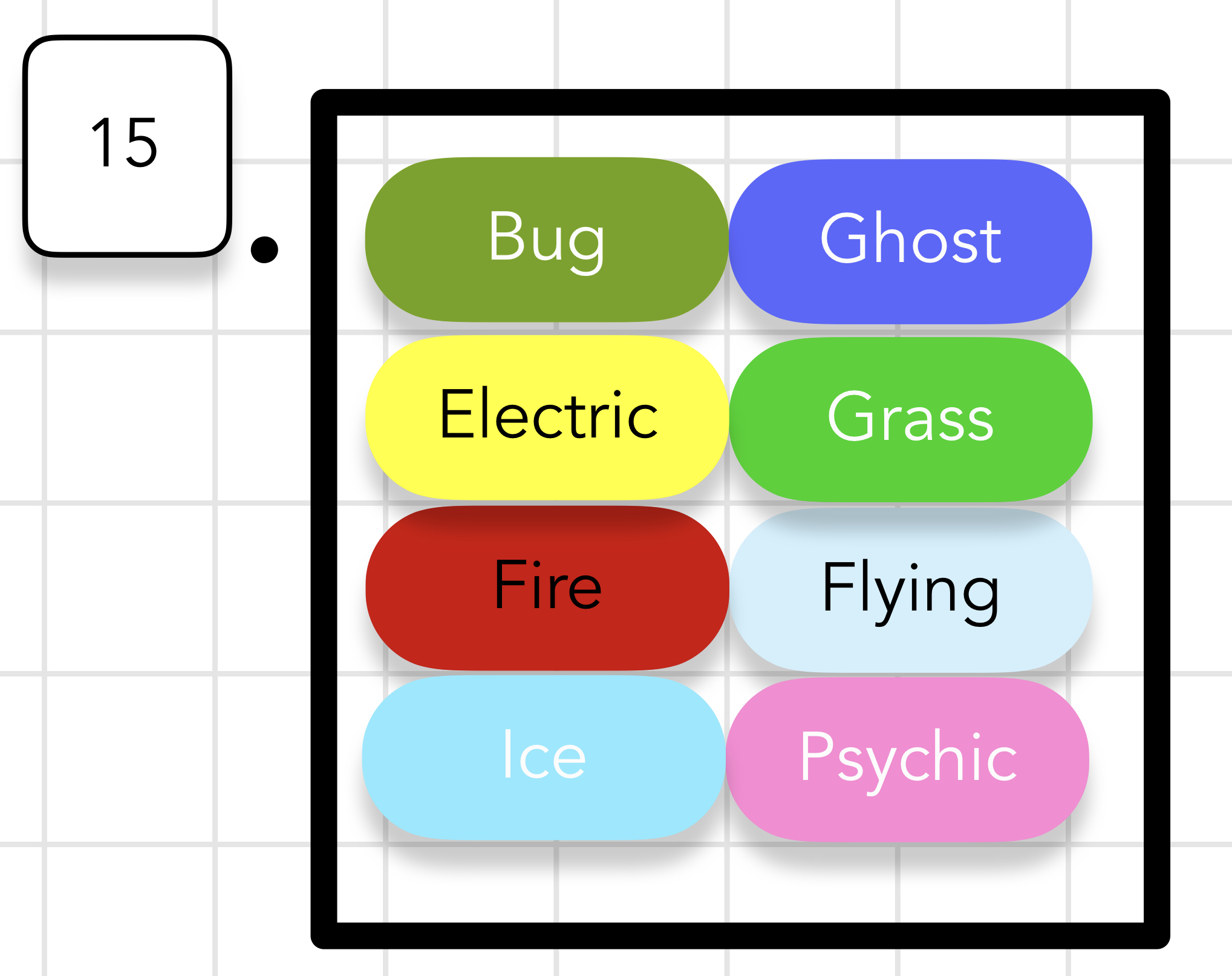
We will use the same types we did for the defensive example, but flip attack and defense.

Here are the key details from the above image.
- Defensive types are the items we must cover with attack types that serve as our options.
- We can only have single attack types. No attack in the game does two simultaneous forms of damage.
- The
Normaltype is not effective against any types in this case. This is possible for many types depending on the size of the sub-problem and simply means we will not choose it as an option. Fun fact: Normal is the only attack type that receives no damage multiplier against other types in the game.
The shrinking of this problem is exactly the same as in the defensive case. Select the item that appears the least across all options and try to cover it first. To expedite things, I will show the exact cover walk across the items that forms the solution.
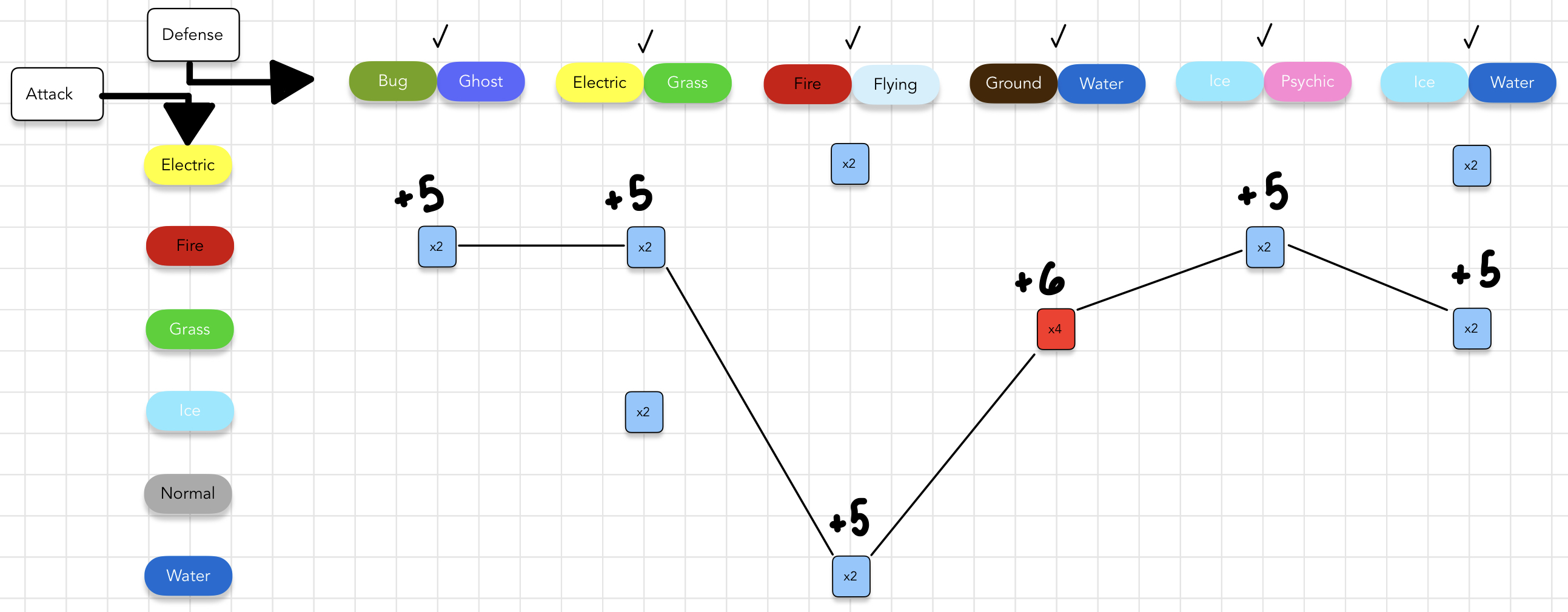
Here are the key details from the above image.
- No two attack types are effective against the same defensive type. Just complete the walk from left to right to see this.
- In addition to selecting our attack types, we can rank them as we decide under the following point system.
- The
x2multiplier is5 points. - The
x4multiplier is6 points. - A HIGHER score is better. This favors stronger attack types for the given defensive items.
- The
- I use this scoring method because I assume quadruple damage is more desirable. A one point difference seems fair if we are only using it to distinguish the quality of the solutions we find.
Again, this ranking system will help when we generate many solutions. Here is the rank of our final picks.
Now that I have summarized how exact cover works for the Pokémon type coverage problem, we can briefly discuss overlapping coverage.
Overlapping Coverage
An exact cover can be difficult to achieve. Depending on the Pokémon generation, it can be impossible. In addition, most people don’t think about being so exact with their choices so that no choice is wasted. Rather, they might just take a sweeping approach, trying to get as much coverage as possible. So, it can be fun to look at cover in a slightly different way, allowing for overlap. With a simple adjustment, we can find many more solutions to graph covering.
Here are the key details from the above image.
- We select the same starting option
Bug-Ghost. - When we cover the items in those options, we leave all other options that contain those items available to solve the cover problem.
By allowing other options to remain available, we end up with a slightly different walk from left to right to solve the problem.
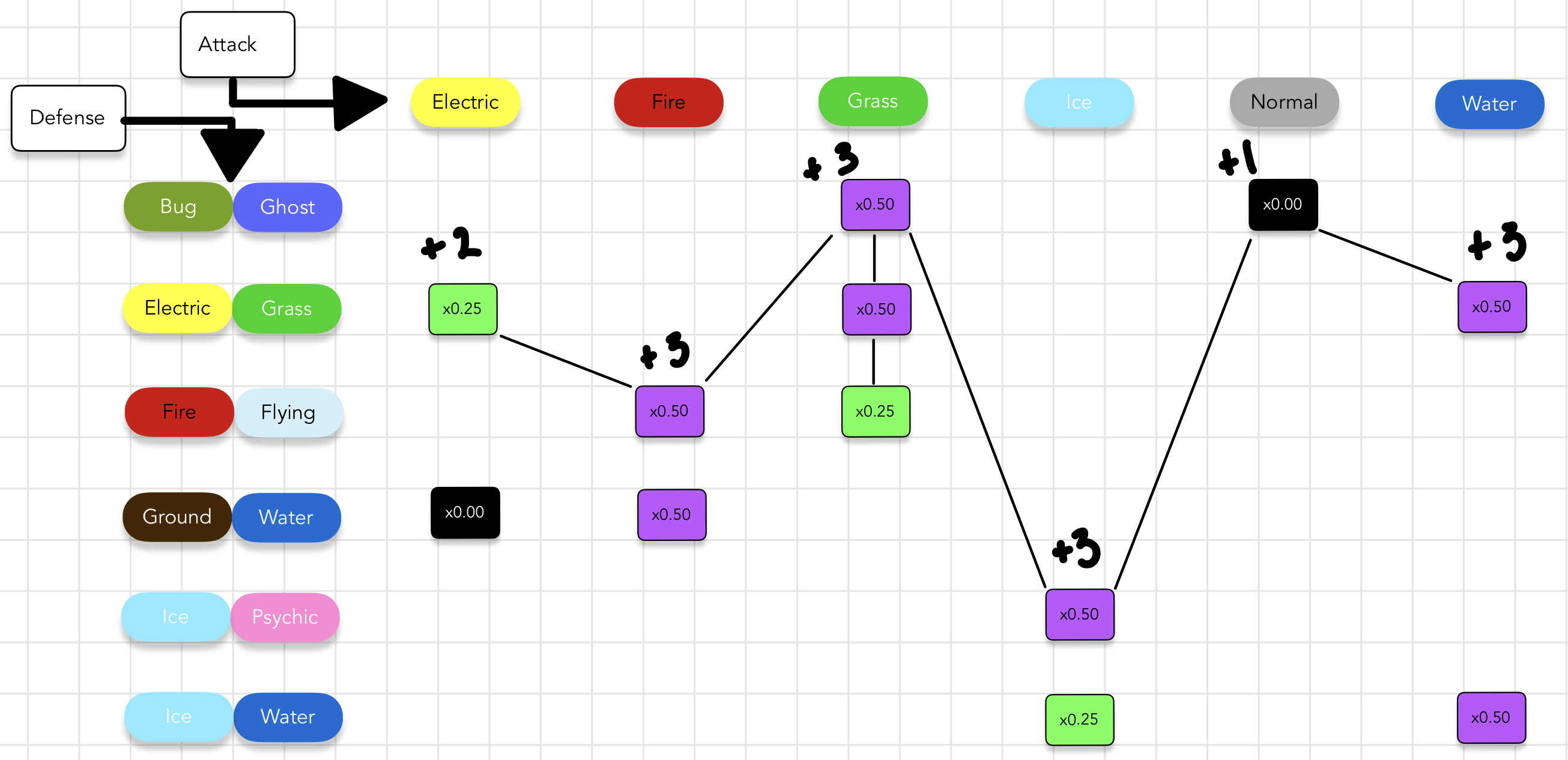
Here are the key details from the above image.
- All scoring systems remain the same as in previous examples.
- Three of our choices for options overlap on the
Grasscoverage. This is acceptable because our goal is to simply cover all attack types within our 6 choice limit.
Here are the results of those choices.
There are a few other overlapping covers within this example if you want to try finding your own to solidify the concepts. You could also try the Attack version, which operates under the exact same principles.
Visualizing a Solution
While drawing out the grid is helpful to test and debug solutions, at its heart dancing links is a graph cover problem. So, we should visualize the solution as a graph, like this.
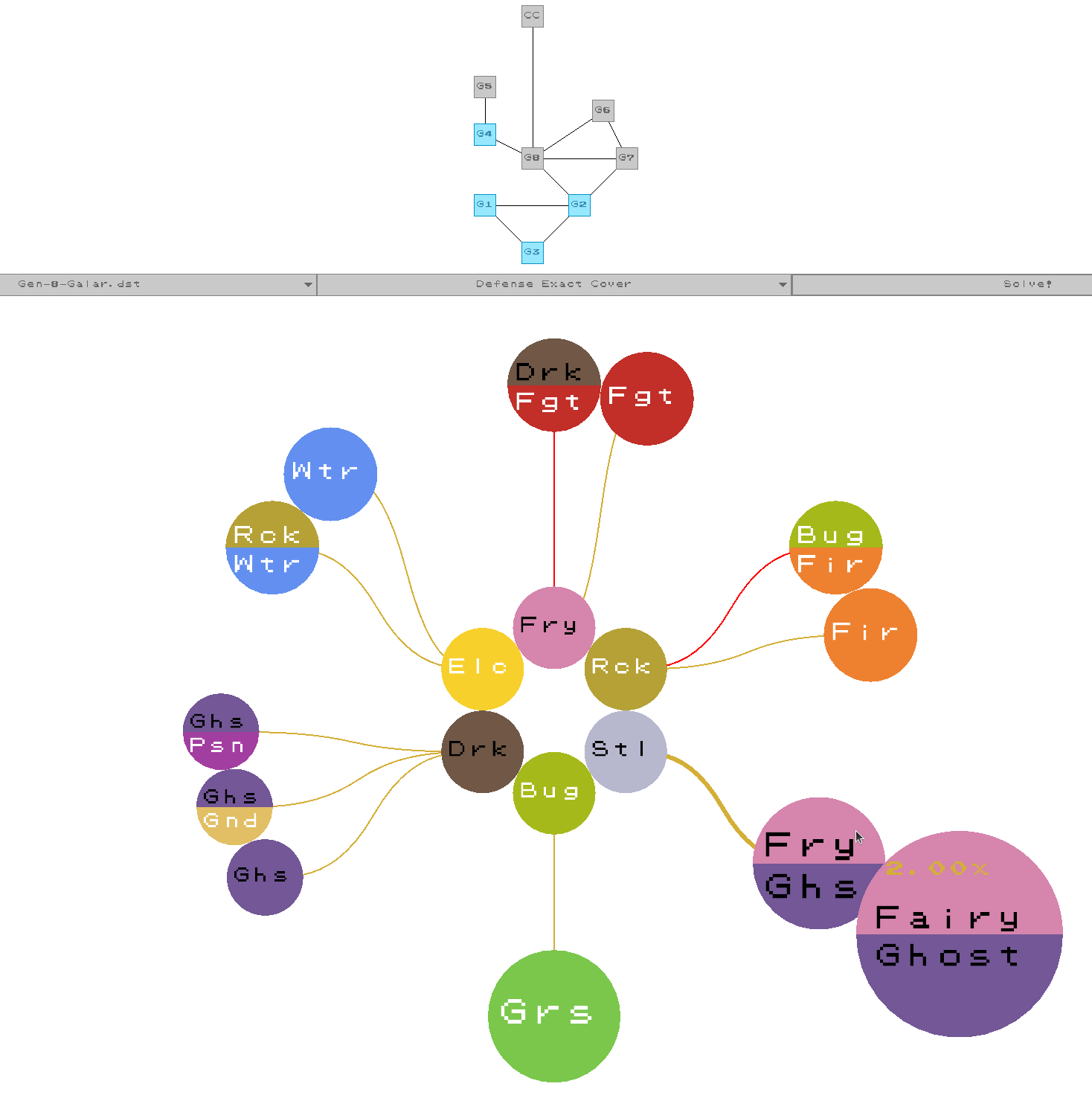
To jump right in to the demo check out the web app demo powered by raylib and Emscripten (for correct mouse tracking enable full screen). Or, visit the repository to build the desktop app locally.
The inner ring of such a visualization can indicate the options we selected to cover the necessary items, which surround the inner ring. Many helpful visualization techniques open up if we decide to display the results in a GUI. For example, the color of the lines indicate the multiplier that each attack type in the inner ring of this example has against the defensive types they cover. For more information, please visit the dancing-links-and-planning-pokemon repository and use the GUI program I wrote to display solutions. Continue reading for more low level implementation details.
Pokémon Planning Implementation
In order to accomplish the in-place, no-copy recursion that comes with Knuth’s Dancing Links, I have chosen to use a C++ vector. In older implementations of Dancing Links, Knuth used a 4-way linked grid of nodes with up, down, left, and right fields. Now, the left-right fields of these nodes can be implicit because we place everything in one vector.
Here is the type that I use to manage the recursion and know when every item is covered. The name corresponds to the item.
struct Type_name
{
Type_encoding name;
uint64_t left;
uint64_t right;
};
std::vector<typeName> headers = {
{"",6,1},
{"Electric",0,2},
{"Fire",1,3},
{"Grass",2,4},
{"Ice",3,5},
{"Normal",4,6},
{"Water",5,0},
};
The Type_encoding is a new addition to this project. Previously, this implementation produced solutions in string format. This means all input and output for the Pokémon types came in the form of std::string. Normally, this would be fine, but the exact cover problem as I have set it up communicates with sets and maps, which means behind the scenes the algorithm is performing thousands if not millions of string comparisons of varying lengths. We can reduce all of these comparisons that are happening to a single comparison between two numbers. This will make moving data faster while vastly reducing the memory footprint. We simply encode all types into this format and get the added benefit of a trivially copy-able class.
class Type_encoding {
public:
Type_encoding() = default;
Type_encoding(std::string_view type);
[[nodiscard]] uint32_t encoding() const;
[[nodiscard]] std::pair<std::string_view, std::string_view>
decode_type() const;
[[nodiscard]] std::pair<uint64_t, std::optional<uint64_t>>
decode_indices() const;
[[nodiscard]] std::string to_string() const;
[[nodiscard]] static std::span<const std::string_view> type_table();
bool operator==(Type_encoding rhs) const;
std::strong_ordering operator<=>(Type_encoding rhs) const;
private:
uint32_t encoding_;
static uint64_t type_bit_index(std::string_view type);
// Any and all Type_encodings will have one global string_view of the type
// strings for decoding.
static constexpr std::array<std::string_view, 18> type_encoding_table = {
// lexicographicly organized table. 17th index is the highest
// lexicographic value "Water."
"Bug", "Dark", "Dragon", "Electric", "Fairy", "Fighting",
"Fire", "Flying", "Ghost", "Grass", "Ground", "Ice",
"Normal", "Poison", "Psychic", "Rock", "Steel", "Water",
};
};
We place every Pokémon type in this uint32_t such that the 0th index bit is Bug and the 17th index bit is Water. In its binary representation, it looks like this.
| Index-Type | Bit Value |
|---|---|
| 0-Bug | 0 |
| 1-Dark | 0 |
| 2-Dragon | 0 |
| 3-Electric | 0 |
| 4-Fairy | 0 |
| 5-Fighting | 0 |
| 6-Fire | 0 |
| 7-Flying | 0 |
| 8-Ghost | 0 |
| 9-Grass | 0 |
| 10-Ground | 0 |
| 11-Ice | 0 |
| 12-Normal | 0 |
| 13-Poison | 0 |
| 14-Psychic | 0 |
| 15-Rock | 0 |
| 16-Steel | 0 |
| 17-Water | 0 |
We now have the ability to turn specific bits on in this type to represent the type we are working with. Turn on one bit for single types and two bits for dual types. For example, “Bug-Water” would be the following.
| Index-Type | Bit Value |
|---|---|
| 0-Bug | 1 |
| 1-Dark | 0 |
| 2-Dragon | 0 |
| 3-Electric | 0 |
| 4-Fairy | 0 |
| 5-Fighting | 0 |
| 6-Fire | 0 |
| 7-Flying | 0 |
| 8-Ghost | 0 |
| 9-Grass | 0 |
| 10-Ground | 0 |
| 11-Ice | 0 |
| 12-Normal | 0 |
| 13-Poison | 0 |
| 14-Psychic | 0 |
| 15-Rock | 0 |
| 16-Steel | 0 |
| 17-Water | 1 |
The final challenge for this strategy is making sure that we can use this type as you would a normal string, in a set or map, for example. This means that the Type_encoding must behave the same as its string representation in terms of lexicographic sorting. To achieve this, the approach aligns the bits in accordance with the lexicographic ordering of the type strings; for example, notice that Bug is the lowest order bit and Water is the highest order bit.
Bug will always be first in terms of lexicographical ordering among these strings. There are some bit counting strategies used to achieve this consistent ordering. For example, we need to ensure that any string that starts with Bug is always sorted before strings that start with a type of higher lexicographic ordering. There are other bit tricks and strategies I use to implement this type efficiently, but you can explore those in the code if you wish. In fact, when compared to a traditional unordered_map that would pre-compute and store all possible encoding and decoding strings, my implementation is faster in both the encoding and decoding phase.
The final optimization involves a recently added C++ type, std::string_view. I try to avoid creating heap allocated strings whenever necessary. Because we must have a table with type names to refer to for the Type_encoding I just point to those strings to display type information when decoding a Type_encoding. I added this constraint to learn more about how to properly use std::string_view and I like the design decisions that followed. See the code for more.
Here is the type that I use within the dancing links array.
struct Poke_link
{
int32_t top_or_len;
uint64_t up;
uint64_t down;
Multiplier multiplier; // x0.0, x0.25, x0.5, x1.0, x2, or x4
int tag; // We use this to efficiently generate overlapping sets.
};
The Multiplier is a simple enum.
enum Multiplier
{
emp = 0,
imm,
f14, // x0.25 damage aka the fraction 1/4
f12, // x0.5 damage aka the fraction 1/2
nrm, // normal
dbl, // double or 2x damage
qdr // quadruple or 4x damage.
};
We then place all of this in one array. Here is an illustration of these links as they exist in memory.
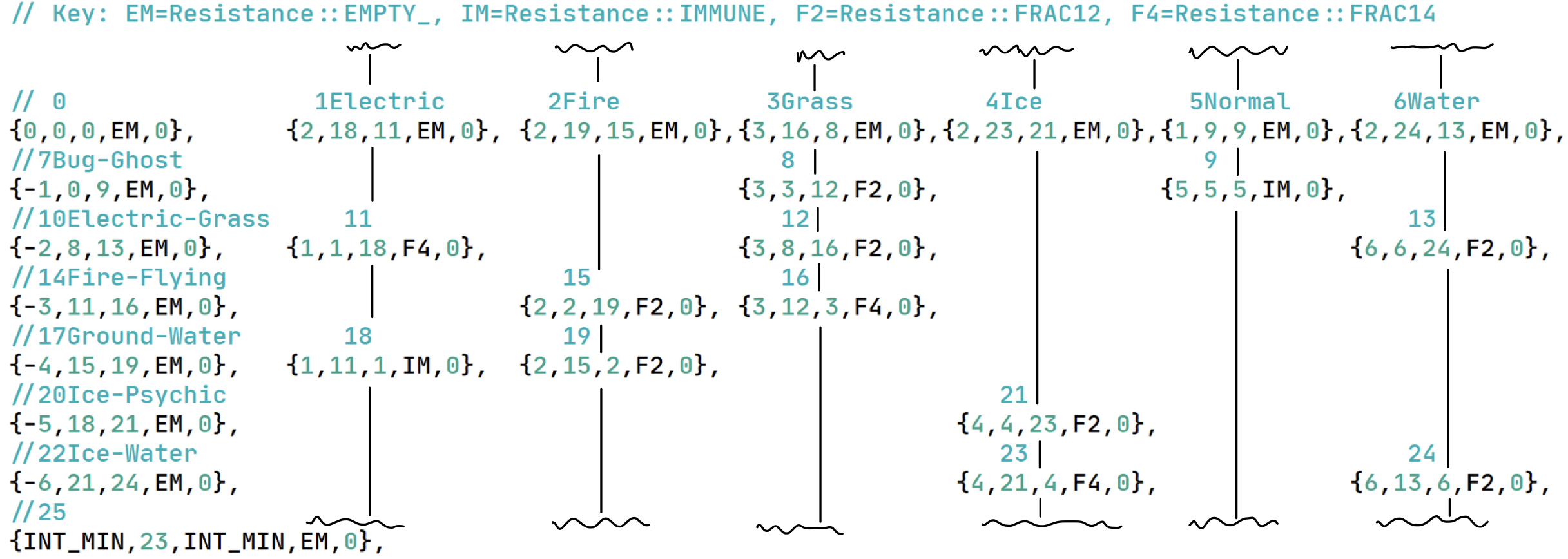
There is also one node at the end of this array to know we are at the end and that our last option is complete. Finally, to help keep track of the options that we choose to cover items, there is another array consisting only of names of the options. These also have an index for the option in the dancing links data structure for some class methods I cover in the next section.
struct Encoding_index
{
Type_encoding name;
uint64_t index;
};
const std::vector<Pokemon_links::Encoding_index> option_table = {
{"", 0},
{"Dragon", 7},
{"Electric", 12},
{"Ghost", 14},
{"Ice", 16},
};
The spacer nodes in the dancing links array have a negative top_or_len field that correspond to the index in this options array, and this array has the index of that option. There are other subtleties to the implementation that I must consider, especially how to use the depth tag to produce overlapping type covers, but that can all be gleaned from the code itself.
A Pokémon Links Class
I wrote this implementation as a class from the beginning. However, early on, I had doubts that this algorithm had any state or attributes that would help justify a class. I could have just as easily wrote a functional algorithm where I take input and provide solutions in my output. However, building the dancing links data structure is non-trivial, so building this structure on every inquiry seemed slow. With a few adjustments, invariants, and runtime guarantees I think there is a case to be made for the Pokémon Links class, and more generally Dancing Links classes for more general algorithms. With minor changes, all the techniques I discuss could be applied to any Dancing Links solver.
Invariants
In order for the following techniques to work we must maintain some invariants in the Dancing Links internals.
- Maintain the identifiers for items–for me this is the
Type_encodingname of the item–in a sorted vector. This is required by Knuth’s algorithms already, but I am adding that the items must be sorted for some later techniques. - Maintain the identifiers for the options–for me this is the
Type_encodingname of the option–in a sorted vector. This is not required by Knuth’s algorithm, but my options have meaningful names that may be different from the item names, so I must make this vector. This will also help with later techniques. - Do not support insertion or deletion of items or options from any data structure. Inserting an item or option may be possible, but it would require substantial modification to the dancing links array that would either be slow or require more space to store the required information. We can support hiding items and options, but not deleting them completely. All operations will be in-place.
Searching
If a user wants to membership test an item or option, we can make some guarantees because we maintain that all items and options are in sorted vectors.
namespace Dancing_links{
[[nodiscard]] bool has_item(Type_encoding item) const;
[[nodiscard]] bool has_option(Type_encoding option) const;
}
has_item—Finding an item isO(log(N))whereNis the number of all items. You cannot find a hidden item.has_option—Finding an option isO(log(N))whereNis the number of all options. You cannot find a hidden option.
Hiding Items
As a part of Algorithm X via Dancing Links, covering items is central to the process. However, with a slightly different technique for hiding items we can give the user the power to temporarily make an item disappear from the world for upcoming inquiries. Here are the hide options we can support.
namespace Dancing_links {
void hide_item(uint64_t header_index);
bool hide_items(Pokemon_links &dlx,
const std::vector<Type_encoding> &to_hide);
bool hide_items(Pokemon_links &dlx,
const std::vector<Type_encoding> &to_hide,
std::vector<Type_encoding> &failed_to_hide);
void hide_items_except(Pokemon_links &dlx,
const std::set<Type_encoding> &to_keep);
}
For the why behind these runtime guarantees, please see the code, but here is what these operations offer.
hide_item—It costsO(log(N))to find one item and a simpleO(1)operation to hide it. The other two options add anO(N)operation to iterate through all requested items. The last overload can report any items that could not be hidden because they were hidden or did not exist in the links.hide_items_except—We must look at all items, however thanks to Knuth’s algorithm the number of items we must examine shrinks if some items are already hidden. It costsO(N * log(K))whereNis not-hidden items andKis the size of the set of items to keep.
Un-hiding Items
The only space complexity cost we incur from hiding an item is that we must remember the order in which items were hidden. If you want to undo the hiding you must do so in precisely the reverse order. While the order does not matter for my implementation, if you had appearances of items across options as nodes with left and right pointers, the order that you spliced them out of options would be important.
To track the order, I use a stack and offer the user stack-like operations that limit how they interact with hidden items.
namespace Dancing_links {
uint64_t num_hid_items(const Pokemon_links &dlx);
Type_encoding peek_hid_item(const Pokemon_links &dlx);
void pop_hid_item(Pokemon_links &dlx);
bool hid_items_empty(const Pokemon_links &dlx);
std::vector<Type_encoding> hid_items(const Pokemon_links &dlx);
void reset_items(Pokemon_links &dlx);
}
Here are the guarantees I can offer for these operations.
num_hid_items/hid_items_empty/peek_hid_items—These are your standard top of the stack operations offeringO(1)runtime. Just as with a normal stack you should not try to peek or pop an empty stack.hid_items—I do provide the additional functionality of viewing the hidden stack for clarity.O(N).pop_hid_item—Luckily, because of some internal implementation choices, un-hiding an item is anO(1)operation. If you were usingleft/rightfields for appearances of items in the options you would need to restore every appearance of those items. But with the tagging technique I use, this is not required in my implementation. This does incur a slight time cost when running a query on the Pokemon Links object if the user has hidden items, but due to the simple nature of traversing an array with indices, and the sparse nature of most matrices, this is a small cost.reset_items—This is anO(H)operation whereHis hidden items.
Hiding Options
We will also use a stack to manage hidden options. Here, however, the stack is required regardless of the implementation technique. We will be splicing options out of the links entirely, requiring that we undo the operation in the reverse order.
namespace Dancing_links {
bool hide_option(Pokemon_links &dlx, Type_encoding to_hide);
bool hide_options(Pokemon_links &dlx,
const std::vector<Type_encoding> &to_hide);
bool hide_options(Pokemon_links &dlx,
const std::vector<Type_encoding> &to_hide,
std::vector<Type_encoding> &failed_to_hide);
void hide_options_except(Pokemon_links &dlx,
const std::set<Type_encoding> &to_keep);
}
Here are the runtime guarantees these operations offer.
hide_option- It costsO(log(N))to find an option andO(I)to hide it, where I is the number of items in an option. The vector version isO(H*I*log(N))whereHis the number of options to hide,Iis the number of items for each option, andNis all options. We can also report back options we could not hide with the last overload. We cannot hide hidden options or options that don’t exist.hide_options_except- This operation will costO(N*log(K)*I)where N is the number of options, K is the size of the set of items to keep, and I is the number of items in an option.
Un-hiding Options
Here are the same stack utilities for the option version of these operations.
namespace Dancing_links {
uint64_t num_hid_options(const Pokemon_links &dlx);
Type_encoding peek_hid_option(const Pokemon_links &dlx);
void pop_hid_option(Pokemon_links &dlx);
bool hid_options_empty(const Pokemon_links &dlx);
std::vector<Type_encoding> hid_options(const Pokemon_links &dlx);
void reset_options(Pokemon_links &dlx);
}
num_hid_options/peek_hid_option/hid_options_empty- standardO(1)stack operations.pop_hid_option-O(I)whereIis the number of items in an option.reset_options-O(HI)whereHis the number of hidden items, andIis the number of items in an option. Usually, we are dealing with sparse matrices, soIhopefully remains low.
Other Operations
With the hiding and un-hiding logic in place you now have a complete set of operations you can use on an in-place data structure that can alter its state and restore the original state when required. Here are the other operations we can use.
namespace Dancing_links {
std::set<Ranked_set<Type_encoding>> exact_cover_functional(Pokemon_links &dlx,
int choice_limit);
std::set<Ranked_set<Type_encoding>> exact_cover_stack(Pokemon_links &dlx,
int choice_limit);
std::set<Ranked_set<Type_encoding>>
overlapping_cover_functional(Pokemon_links &dlx, int choice_limit);
std::set<Ranked_set<Type_encoding>> overlapping_cover_stack(Pokemon_links &dlx,
int choice_limit);
}
We are now able to solve cover problems on a Pokemon_links object that is in a user-defined, altered state. The user can modify the structure as much as they would like and restore it to its original state with minimal internal maintenance of the object required. With the decent runtime guarantees we can offer with this data structure, the memory efficiency, lack of copies, and flexible state, I think there is a strong case to be made for a class implementation of Dancing Links.
Treating the Pokemon_links as an alterable object with a prolonged lifetime can be useful in GUI and CLI programs in this repo. For each Pokémon map I load in, I only load two Pokemon_links objects, one for ATTACK and one for DEFENSE. As the user asks for solutions to only certain sets of gyms, we simply hide the items the user is not interested in and restore them after every query. I have not yet found a use case for hiding options but this project could continue to grow as I try out different techniques.
Conclusion
I hope you enjoyed this deep dive on how to apply Donald Knuth’s Dancing Links solver to Pokémon teams. I found it tremendously satisfying to abstract a beloved childhood game of mine into a form that was solvable by an algorithm I found interesting.
For another perspective on the directed graph that is the Pokémon type advantage network, see this great video by creator Not David, “The Pokemon Type Advantage Network”. This video helped me start thinking about different ways to model the type interactions in these games.
For the full implementation of this project that solves the cover problems we discussed, across nine Pokémon generations, please visit my GitHub repository.